john henry newman
A thoughtful essay on Newman... Eamon Duffy reviewing John Cornwell's biography.
A remarkably consistent thinker, to the end of his life Newman looked back on his conversion to evangelical Protestantism in 1816 as the saving of his soul. Yet as a fellow of Oriel, the most intellectually prestigious of the Oxford colleges, he outgrew his earlier Calvinism. He came to see Evangelicalism, with its emphasis on religious feeling and on the Reformation doctrine of justification by faith alone, as a Trojan horse for an undogmatic religious individualism that ignored the Church’s role in the transmission of revealed truth, and that must lead inexorably to subjectivism and skepticism.
Partly as an antidote to his own instinctive skepticism, Newman sought objective religious truth initially in a romanticized version of the Anglican High Church tradition, emphasizing the mystery of God, the beauty and necessity of personal holiness, and the centrality of the Church’s sacraments and teaching for salvation. He was ordained as a priest in 1824, and in 1831 was appointed preacher to the university. Eloquent, learned, widely read, combining a beautiful voice with an unmatched mastery of words, by the early 1830s Newman had acquired a cult following in Oxford. Admiring undergraduates imitated even his eccentricities, like his habit of kneeling down abruptly as if his knees had given way.
The university authorities were alarmed at his growing influence, and changed college mealtimes so that undergraduates had to choose between hearing Newman preach and eating their dinners. In their hundreds, they chose the preaching. This was all the more remarkable since Newman’s message was both uncompromisingly austere and often deliberately provocative, as in his declaration that “it would be a gain to this country, were it vastly more suspicious, more bigoted, more gloomy, more fierce in its religion, than at present it shows itself to be.”
via The New York Review of Books.
But by the early 1840s, Newman himself had lost confidence in it. His increasingly subtle attempts to interpret the foundation documents of the Church of England in ways compatible with Roman Catholic teaching provoked a hostile backlash both from the Anglican bishops and from older and more cautious High Churchmen.
Frustrated by the apparently impregnable Protestantism of their contemporaries, one by one Newman’s more headstrong disciples became Roman Catholics. Newman did what he could to stem the leakage, but was himself in an agony of indecision, increasingly convinced that Rome possessed the fullness of truth, yet unable to bring his loyalties and emotions into accord with his intellect. “Paper logic” was merely the trace of deeper and more mysterious movements of heart and mind. As he wrote later, recalling this long slow “death-bed” as an Anglican:
It is the concrete being that reasons; pass a number of years, and I find my mind in a new place; how? The whole man moves…. Great acts take time. He resigned his university pulpit and retreated to Littlemore, a village outside Oxford where he had built a church. There he and a dwindling band of followers lived a quasi-monastic life of prayer, fasting, and reflection. In October 1845 Newman at last recognized where his own logic had led him, and was received into the Roman Catholic Church.
Both Newman’s attraction to Catholicism and his hesitation in embracing it sprang from a radical historicism. As an Anglican, he had subscribed to the notion that truth was unchanging. Christianity was a revealed religion, its doctrines descended to the present in an unbroken tradition from the Apostles. Nothing could count as Christian truth, unless the primitive Church had believed and taught it. The modern Church of Rome, therefore, could not claim to be the true Church, since so much about it—its elaborate worship, the dominant place of the Virgin Mary in its piety, the overweening authority of the pope—seemed alien or absent from the earliest Christianity: there were no rosary beads in third-century Carthage. Yet Newman’s reading in early Christian sources convinced him that to condemn Rome on these grounds would also be to outlaw much of the rest of mainstream Christianity. The doctrines of Incarnation and Trinity, accepted as fundamental by both Catholics and Protestants, were not to be found in their mature form in the early Church. If the central tenets of the faith could develop legitimately beyond their New Testament foundations, why not everything else?
To resolve this apparent contradiction between a religion of objectively revealed truth and the flux of Christian doctrines and practices, Newman wrote at Littlemore a theological masterpiece, the Essay on the Development of Christian Doctrine (1845). Its central claim is that the concepts and intuitions that shape human history are dynamic, not inert. Great ideas interact with changing times and cultures, retaining their distinctive thrust and direction, yet adapting so as to preserve and develop that energy in different circumstances. Truth is a plant, evolving from a seed into the mature tree, not a baton passed unchanging from hand to hand. Ideas must unfold in the historical process before we can appropriate all that they contain. So beliefs evolve, but they do so to preserve their essence in the flux of history: they change, that is, in order to remain the same. “In a higher world it is otherwise; but here below to live is to change, and to be perfect is to have changed often.”
banning chinglish
China has banned newspapers, publishers and website-owners from using foreign words - particularly English ones. China's state press and publishing body said such words were sullying the purity of the Chinese language.
It said standardised Chinese should be the norm: the press should avoid foreign abbreviations and acronyms, as well as "Chinglish" - which is a mix of English and Chinese.
via BBC News.
all else being equal
The etymology of the word equal is from the Latin word aequalis, meaning "uniform, identical, or equal," from aequus "level, even, just." The "=" symbol that is now universally accepted by mathematics for equality was first recorded by Welsh mathematician Robert Recorde in The Whetstone of Witte (1557). The original form of the symbol was much wider than the present form. In his book Recorde explains his design of the "Gemowe lines" (meaning twin lines, from the Latin gemini):
...to auoide the tediouſe repetition of theſe woordes : is equalle to : I will ſette as I doe often in woorke vſe, a paire of paralleles, or Gemowe lines of one lengthe, thus: =, bicauſe noe .2. thynges, can be moare equalle.
...to avoid the tedious repetition of these words: "is equal to", I will set (as I do often in work use) a pair of parallels (or Gemowe[1] lines) of one length (thus =), because no two things can be more equal.
via Wikipedia.
australian summer
THONGS and board shorts gave way to beanies and scarves yesterday as summer gave way to a wintry blast of snow and icy temperatures in the country's southeast.
While the bitter freeze in Europe continues, Victoria and NSW have had a cold snap of their own, with off-season ski slopes transformed into winter wonderlands.
About 30cm of snow fell at Perisher in NSW yesterday, while Victoria's Mount Hotham received a 10cm dusting on Sunday.
Charlotte's Pass in the NSW Snowy Mountains also received a 10cm sprinkling of snow, prompting would-be bushwalkers to don clothing more suitable for skiing.
via News.com.au.
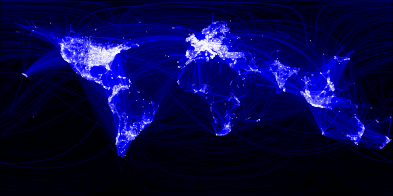
visualizing friendships: facebook
Visualizing data is like photography. Instead of starting with a blank canvas, you manipulate the lens used to present the data from a certain angle.
When the data is the social graph of 500 million people, there are a lot of lenses through which you can view it. One that piqued my curiosity was the locality of friendship. I was interested in seeing how geography and political borders affected where people lived relative to their friends. I wanted a visualization that would show which cities had a lot of friendships between them.
I began by taking a sample of about ten million pairs of friends from Apache Hive, our data warehouse. I combined that data with each user's current city and summed the number of friends between each pair of cities. Then I merged the data with the longitude and latitude of each city.
At that point, I began exploring it in R, an open-source statistics environment. As a sanity check, I plotted points at some of the latitude and longitude coordinates. To my relief, what I saw was roughly an outline of the world. Next I erased the dots and plotted lines between the points. After a few minutes of rendering, a big white blob appeared in the center of the map. Some of the outer edges of the blob vaguely resembled the continents, but it was clear that I had too much data to get interesting results just by drawing lines. I thought that making the lines semi-transparent would do the trick, but I quickly realized that my graphing environment couldn't handle enough shades of color for it to work the way I wanted.
Instead I found a way to simulate the effect I wanted. I defined weights for each pair of cities as a function of the Euclidean distance between them and the number of friends between them. Then I plotted lines between the pairs by weight, so that pairs of cities with the most friendships between them were drawn on top of the others. I used a color ramp from black to blue to white, with each line's color depending on its weight. I also transformed some of the lines to wrap around the image, rather than spanning more than halfway around the world.
via Facebook.
the bigger number
Lucid and fascinating essay from Scott Aaronson:
In an old joke, two noblemen vie to name the bigger number. The first, after ruminating for hours, triumphantly announces "Eighty-three!" The second, mightily impressed, replies "You win."A biggest number contest is clearly pointless when the contestants take turns. But what if the contestants write down their numbers simultaneously, neither aware of the other’s? To introduce a talk on "Big Numbers," I invite two audience volunteers to try exactly this. I tell them the rules:
You have fifteen seconds. Using standard math notation, English words, or both, name a single whole number—not an infinity—on a blank index card. Be precise enough for any reasonable modern mathematician to determine exactly what number you’ve named, by consulting only your card and, if necessary, the published literature.
So contestants can’t say "the number of sand grains in the Sahara," because sand drifts in and out of the Sahara regularly. Nor can they say "my opponent’s number plus one," or "the biggest number anyone’s ever thought of plus one"—again, these are ill-defined, given what our reasonable mathematician has available. Within the rules, the contestant who names the bigger number wins.
Are you ready? Get set. Go.